Binary Search Tree
Binary Search Tree
Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
- It is called a Binary tree because each tree node has a maximum of 2 children
- It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.
The properties that separates a binary search tree from a regular binary tree is
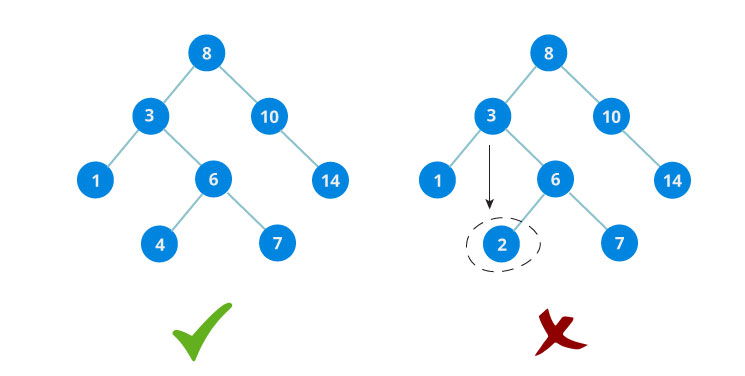
On the picture shown above, the right tree is not a binary search tree because on the right subtree of the root, there's a number with smaller value than the root.
- All nodes of left subtree are less than root node
- All nodes of right subtree are more than root node
- Both subtrees of each node are also BSTs meaning they have the above two properties

On the picture shown above, the right tree is not a binary search tree because on the right subtree of the root, there's a number with smaller value than the root.
Basic Operations
Following are the basic operations of a tree −
- Search − Searches an element in a tree.
- Insert − Inserts an element in a tree.
- Pre-order Traversal − Traverses a tree in a pre-order manner.
- In-order Traversal − Traverses a tree in an in-order manner.
- Post-order Traversal − Traverses a tree in a post-order manner.
Search Operation
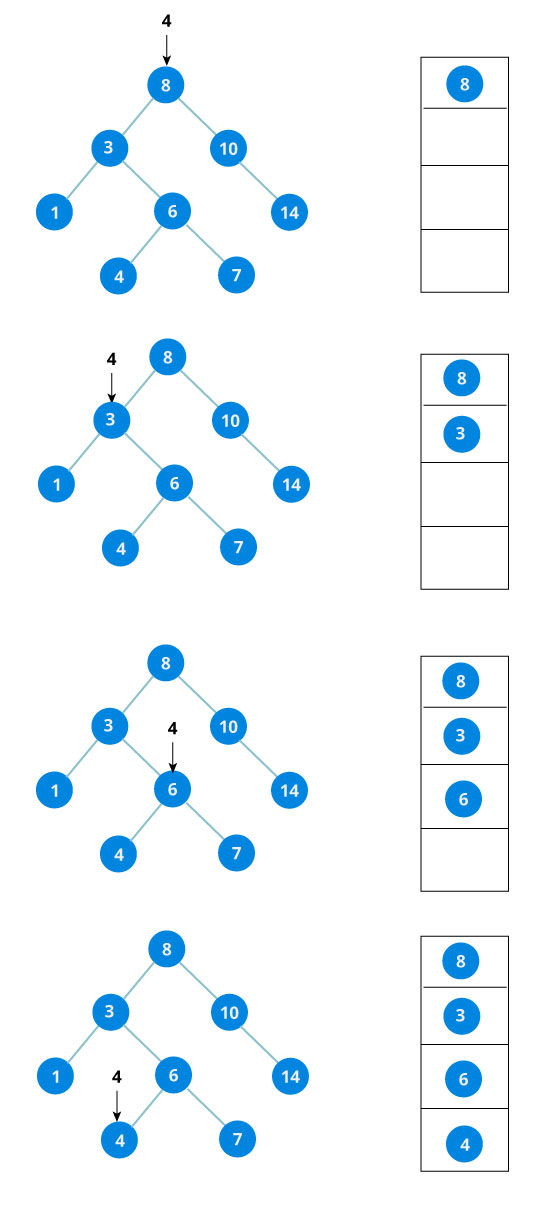
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Algorithm
struct node* search(int data){ struct node *current = root; printf("Visiting elements: "); while(current->data != data){ if(current != NULL) { printf("%d ",current->data); //go to left tree if(current->data > data){ current = current->leftChild; } //else go to right tree else { current = current->rightChild; } //not found if(current == NULL){ return NULL; } } } return current; }
Here's the visualization diagram:
Insert Operation
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
Algorithm
void insert(int data) { struct node *tempNode = (struct node*) malloc(sizeof(struct node)); struct node *current; struct node *parent; tempNode->data = data; tempNode->leftChild = NULL; tempNode->rightChild = NULL; //if tree is empty if(root == NULL) { root = tempNode; } else { current = root; parent = NULL; while(1) { parent = current; //go to left of the tree if(data < parent->data) { current = current->leftChild; //insert to the left if(current == NULL) { parent->leftChild = tempNode; return; } } //go to right of the tree else { current = current->rightChild; //insert to the right if(current == NULL) { parent->rightChild = tempNode; return; } } } } }
Here's the visualization diagram:
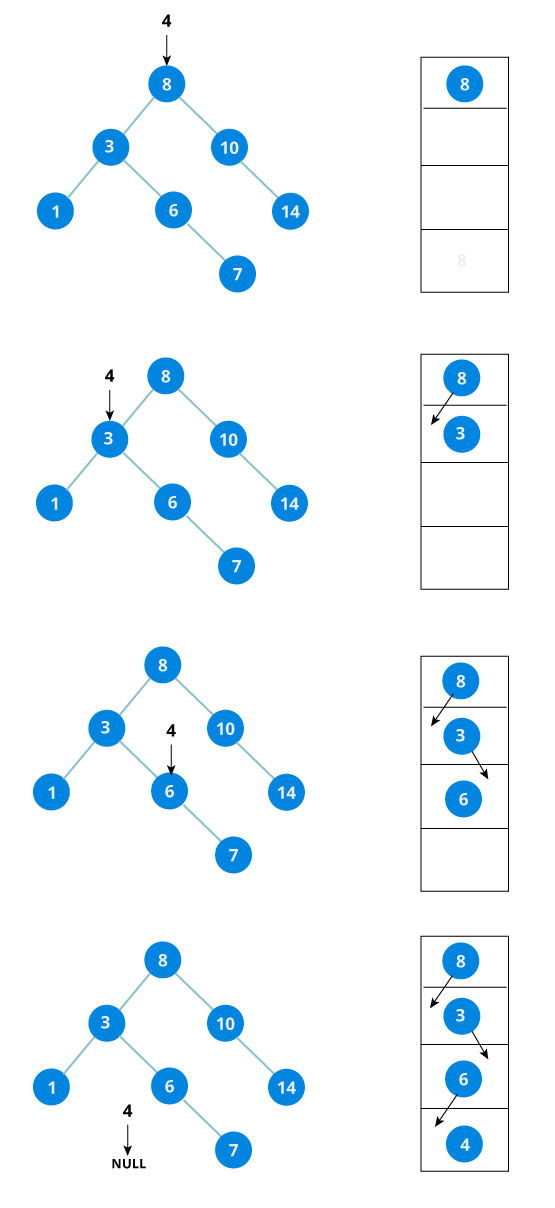
We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
https://www.tutorialspoint.com/data_structures_algorithms/binary_search_tree.htm
Comments
Post a Comment