AVL Tree & B - Tree

AVL Tree


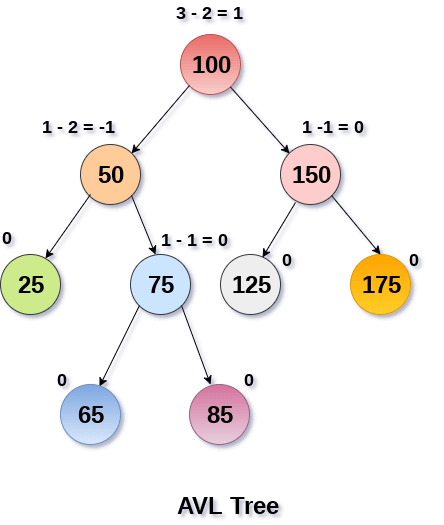
AVL tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1.

AVL tree got its name after its inventor Georgy Adelson-Velsky and Landis. Since AVL trees are height balance trees, operations like insertion and deletion have low time complexity.

AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor.



Balance Factor

  • Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node
  • Balance Factor = (Height of Left Subtree - Height of Right Subtree) or (Height of Right Subtree - Height of Left Subtree)
  • The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1.
  • If the difference in the height of left and right sub-trees is more than 1, the tree is balanced using some rotation techniques.
AVL Tree
We can see that the balance factor associated with each node is in between -1 and +1. Therefore, it is an example of AVL tree. (https://www.javatpoint.com/avl-tree)

Rotation Techniques

(Taken from https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm)
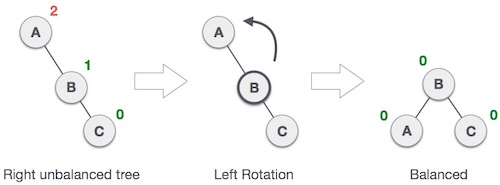
  • Left rotation (Single rotation)
If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation −
Left Rotation
In our example, node A has become unbalanced as a node is inserted in the right subtree of A's right subtree. We perform the left rotation by making A the left-subtree of B.

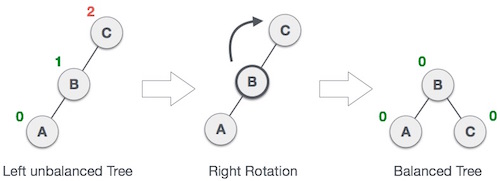
  • Right rotation (Single rotation)
AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.
Right Rotation
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.

  • Left-Right rotation (Double rotation)
Double rotations are slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let's first check how to perform Left-Right rotation. A left-right rotation is a combination of left rotation followed by right rotation.
StateAction
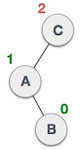Right RotationA node has been inserted into the right subtree of the left subtree. This makes C an unbalanced node. These scenarios cause AVL tree to perform left-right rotation.
Left Rotation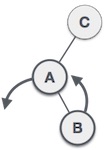We first perform the left rotation on the left subtree of C. This makes A, the left subtree of B.
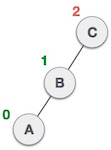Left RotationNode C is still unbalanced, however now, it is because of the left-subtree of the left-subtree.
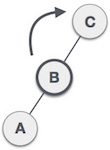Right RotationWe shall now right-rotate the tree, making B the new root node of this subtree. C now becomes the right subtree of its own left subtree.
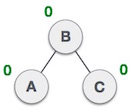Balanced Avl TreeThe tree is now balanced.
  • Right-Left rotation (Double rotation)
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.
StateAction
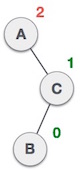Left Subtree of Right SubtreeA node has been inserted into the left subtree of the right subtree. This makes A, an unbalanced node with balance factor 2.
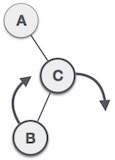Subtree Right RotationFirst, we perform the right rotation along C node, making C the right subtree of its own left subtree B. Now, B becomes the right subtree of A.
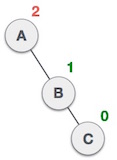Right Unbalanced TreeNode A is still unbalanced because of the right subtree of its right subtree and requires a left rotation.
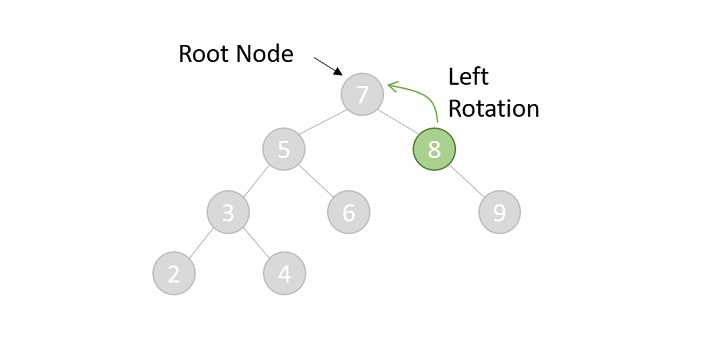Left RotationA left rotation is performed by making B the new root node of the subtree. A becomes the left subtree of its right subtree B.
Balanced AVL TreeThe tree is now balanced.

Operations

Insertion

An insertion in AVL tree is similar to a normal Binary Search Tree insertion. After inserting, we need to fix the AVL  tree using the learned rotations.

  • If there is an imbalance in left child of right subtree, then you perform a left-right rotation.
  • If there is an imbalance in left child of left subtree, then you perform a right rotation.
  • If there is an imbalance in right child of right subtree, then you perform a left rotation.
  • If there is an imbalance in right child of left subtree, then you perform a right-left rotation.

Deletion

Deletion can also be performed in the same way as it is performed in a binary search tree. Deletion may also disturb the balance of the tree therefore, various types of rotations are used to rebalance the 

Examples




 B Tree

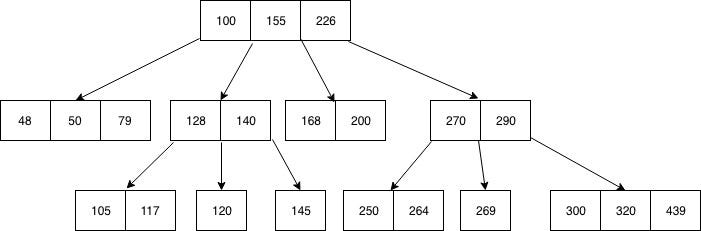
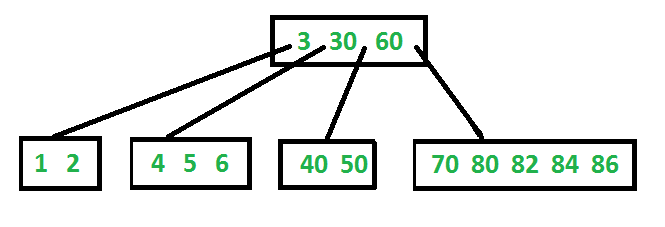
B Tree is another type of a self-balancing tree.We can represent sample B-tree as follows.


B-Tree is a self-balanced search tree in which every node contains multiple keys and has more than two children.

B-Tree of Order m has the following properties...

Property #1 - All leaf nodes must be at same level.
Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
Property #4 - If the root node is a non leaf node, then it must have at least 2 children.
Property #5 - A non leaf node with n-1 keys must have n number of children.
Property #6 - All the key values in a node must be in Ascending Order.

For example, B-Tree of Order 4 contains a maximum of 3 key values in a node and maximum of 4 children for a node.

BTreeIntro

Operations

1. Search
Search is similar to the search in Binary Search Tree. Let the key to be searched be k. We start from the root and recursively traverse down. For every visited non-leaf node, if the node has the key, we simply return the node. Otherwise, we recur down to the appropriate child (The child which is just before the first greater key) of the node. If we reach a leaf node and don’t find k in the leaf node, we return NULL.

2. Insertion
In a B-Tree, a new element must be added only at the leaf node. That means, the new key Value is always attached to the leaf node only. The insertion operation is performed as follows...

Step 1 - Check whether tree is Empty.
Step 2 - If tree is Empty, then create a new node with new key value and insert it into the tree as a root node.
Step 3 - If tree is Not Empty, then find the suitable leaf node to which the new key value is added using Binary Search Tree logic.
Step 4 - If that leaf node has empty position, add the new key value to that leaf node in ascending order of key value within the node.
Step 5 - If that leaf node is already full, split that leaf node by sending middle value to its parent node. Repeat the same until the sending value is fixed into a node.
Step 6 - If the splitting is performed at root node then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Comments

Post a Comment

Popular posts from this blog

Binary Search Tree

Image
Binary Search Tree Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.  It is called a Binary tree because each tree node has a maximum of 2 children It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time. The properties that separates a binary search tree from a regular binary tree is All nodes of left subtree are less than root node All nodes of right subtree are more than root node Both subtrees of each node are also BSTs meaning they have the above two properties On the picture shown above, the right tree is not a binary search tree because on the right subtree of the root, there's a number with smaller value than the root.  Basic Operations Following are the basic operations of a tree − Search   − Searches an element in a tree. Insert  − Inserts an element in a tree. Pre-order Traversal  − Traverses a tree in a pre-order manner...
Read more

Hashing Table & Binary Tree

Image
Hashing Table Hash Table is a data structure which stores data in an associative manner.  Data is stored in an array format, where each data value has its own unique index value.  Access of data becomes very fast if we know the index of the desired data. So,   Hash Table is a data structure in which insertion and search operations are very fast where the size of the data doesn't matter.   Hash Function  A hash function job is to store values in an array with a limited size It does it in a way that the array doesn't need to be searched through to find it. This allows us to enter values in any order and we can find them using a calculation instead of searching through the array So how does Hash Table & Hash Function work together? Key values are assigned to elements in a Hash Table using a Hash Function Hash function helps calculate the best index an item should go in Here are a few methods to hash  keys  from string: Mid...
Read more